I came across a neat video, via Jennifer Ouellette, where a couple of MIT students re-enact a classic physics textbook problem. It’s a problem that I first heard over a decade ago, when I was in high school, and is one of the few physics 101 problems to have earned the distinction of its own wikipedia page.
See MIT physics students do the famous "Monkey and a Gun" demonstration with a golf ball gun, and a stuffed monkey. http://t.co/fOe1RGuDLA
— Jennifer Ouellette (@JenLucPiquant) June 21, 2013
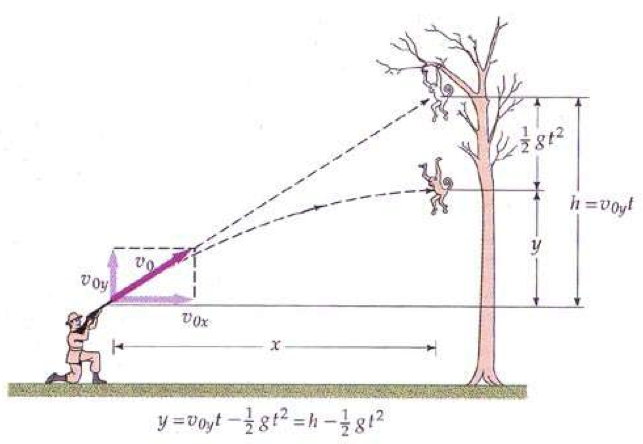
Here’s the setup. A monkey hangs from a branch of a tree. A hunter aims their rifle at a monkey. At the very instant the hunter pulls the trigger, the monkey gets startled by the sound, lets go of the branch, and falls from the tree. The question is: will the bullet still hit the monkey? If not, where should the hunter have aimed the gun to hit the monkey?

So, do you think the hunter should aim the gun:
- Above the monkey?
- At the monkey?
- Below the monkey?
Before reading on, take a moment to come up with your answer.
Thought about it?
This problem has somewhat of an amusing legacy. In an effort to revamp physics problems to fit more environmentally enlightened times, textbook authors have taken great pains to distance themselves from the barbaric act of shooting monkeys on trees.
Here’s the original version of the problem, from 1971, featuring a hunter and a monkey.
Compare that to a modern variant, this one from 2000, featuring a distressed zookeeper who’s trying to coax an escaped monkey to climb down a tree. In the words of the authors, “After failing to entice the monkey down, the zoo keeper points her tranquilizer gun directly at the monkey and shoots.” If this is still a little alarming, some versions feature a friendly naturalist in place of the distressed zookeeper.

Here’s someone trying to feed a monkey a banana (I doubt the zookeeper would approve).
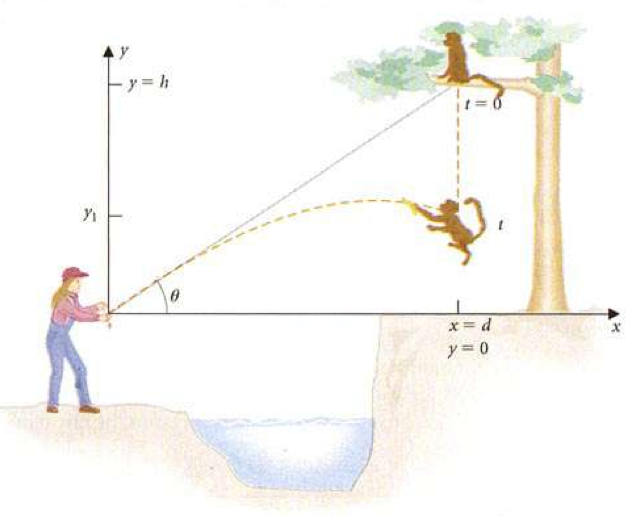
By the time I came across this problem, it had become somewhat more convoluted. I mean, well.. just look at the figure.

I believe what we have here is someone blowing into a pea shooter that shoots out tiny spherical magnets, which can then stick to a falling metal can. The can is somehow wired to fall at the exact moment she launches the magnet. You know, just your every-day magnetic pea shooter wired to a falling-metal-can scenario.
And that isn’t even the strangest version of the problem I’ve come across. That honor goes to this next version. See if you can figure out what’s going on from the figure.
This is, of course, the less famous cousin of William Tell, who decided to shoot a coconut with an arrow. Oh, and the coconut happens to be held by a monkey. Unfortunately, the monkey is a somewhat unreliable stooge, and the moment the archer releases the arrow, the monkey lets go of the coconut. Silly monkey, you had one job! Just hold the darn coconut.
Needless to say, these figures are starting to get a little visually jarring, and perhaps detracting from the key physics principle.
The latest version of this age-old conundrum comes to you from two MIT students, who wired a sock puppet monkey to fall at the exact moment a golf ball cannon is fired. I decided to track the motion of the ball and the monkey in the video. Before watching the video, think back to your prediction.
Isn’t that neat? Even though the golf ball curves away from its aimed trajectory, it still hits the monkey dead on!
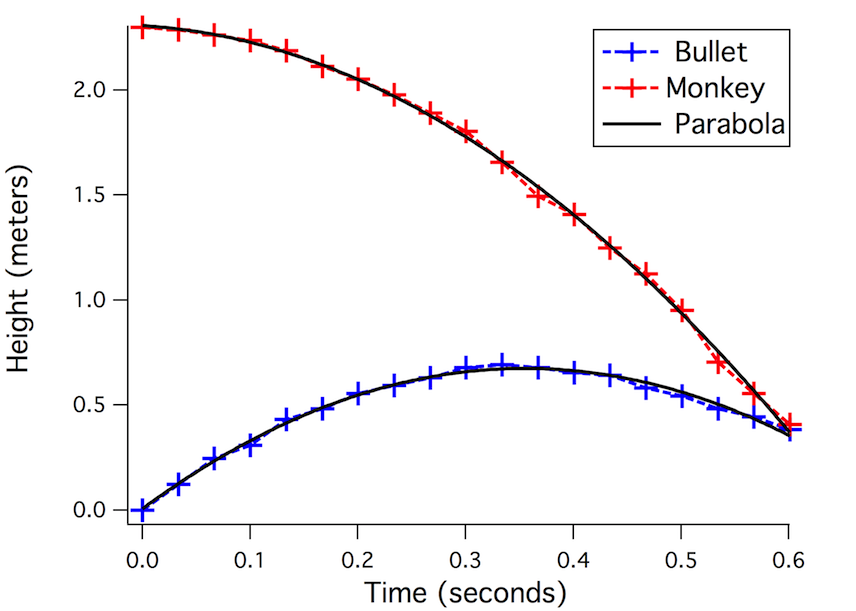
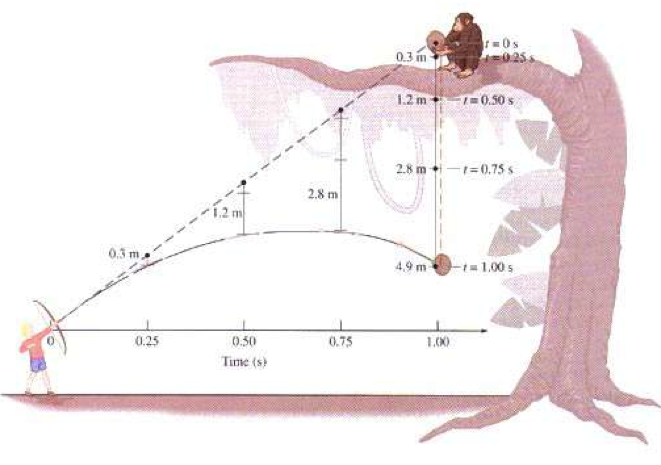
So why did this happen? First, look at the light blue curve above. The monkey falls downwards in a straight line. But say you were to plot the height of the monkey, measured from the ground, as it changed over time. What would that plot look like? If you haven’t seen this before, it’s kind of surprising.
What you see is that even objects that fall in a straight line trace out a neat curve, called a parabola, when you plot their height versus time. The red curve is the monkey’s trajectory, recorded from the video, and the black line is a curve representing a perfect parabola. See how nicely they line up! Physics isn’t just textbook stuff.
Now, let’s add the height of the bullet into this picture:
Again, notice how well the bullet’s motion lines up with a parabola. This is the sort of thing that I find very cool about physics – you can abstract away the monkey, and discover a mathematical world that’s hiding beneath.
When I look at this curve above, it strikes me a pretty startling that those two curves intersect. It seems like a cosmic coincidence that the bullet managed to hit the monkey. But this isn’t the whole picture.
Let’s imagine for a moment what would happen in a world without gravity. The bullet would just keep moving in a straight line path. Let’s call this the aiming line. The monkey would still be up in the tree (since it can’t fall without gravity). It’s obviously going to be a bulls-eye shot.
Now, switch on gravity. The bullet curves away from its original, intended path (the aiming line, shown in green in the above video). And the monkey falls from its perch. But here’s the kicker: both the bullet and monkey deviate from their original paths at exactly the same rate. What I mean is this: if at any moment, you measure how far the bullet has dropped below the green line, and at that exact moment, you measure how far the monkey has fallen from its perch, those two distances will be exactly the same.
The bullet and the monkey both ‘missed’ the branch, but they missed it by exactly the same amount! If you think about it, this single fact means that they are still going to collide.
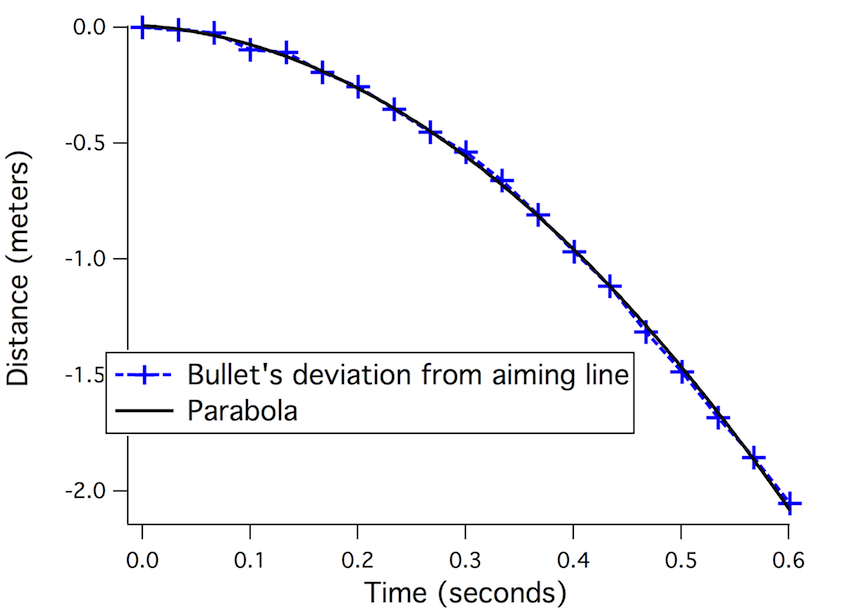
Let’s try it out and see if it works. Let’s measure how far the bullet strays from its original green aiming line. Here’s what this deviation looks like:
Surprisingly, it’s still a parabola, but a different parabola from before (in technical terms, we’ve subtracted off the linear term).
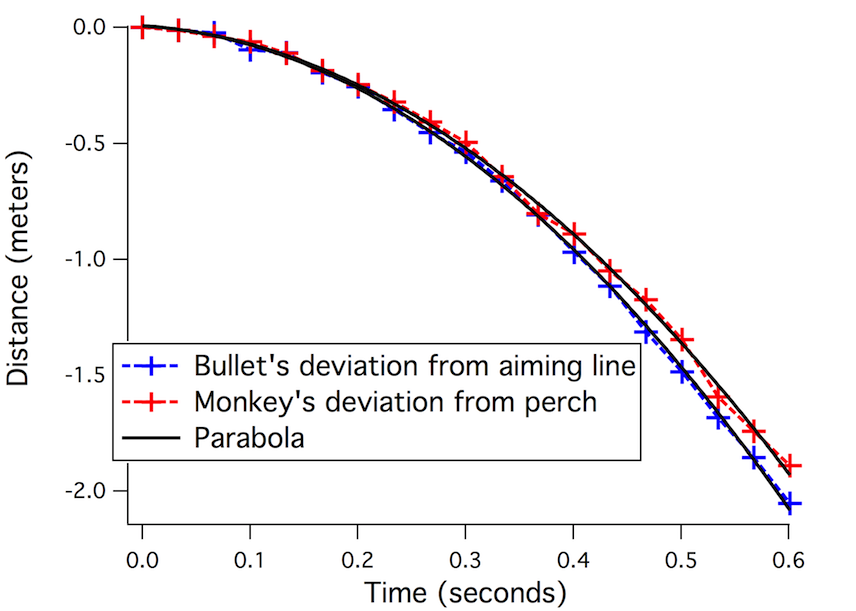
Now, we can do the same thing for the monkey. At zero seconds, the monkey sits on the perch. A tenth of a second later, it’s a few centimeters below the perch. Another tenth of a second and it falls further still. Let’s take this curve – the monkey’s deviation from its perch – and overlap it with the bullet’s deviation from the aiming line.
What do you know, it lines up pretty neatly.
This is why the bullet hits the monkey, why the archer hits the coconut, or why the magnet hits the tin can. It’s because the Earth affects the motion of all falling objects in exactly the same way. No matter what you throw – coconuts, peas, golf balls, or bullets – they all deviate from their ‘aiming line’ at exactly the same rate. All falling objects play by exactly the same rules.
Footnotes:
In reality, a target rarely drops out of a tree the moment you fire a gun. In fact, gun manufacturers already take into account the fact that bullets fall. When you set the sight on a rifle, what you’re really doing is correcting for how far the bullet will fall by the time it hits its target.
The many variants of the hunter-monkey problem above are from the slides of an excellent talk by Eric Mazur where he emphasizes the importance of using simple, non-distracting figures.
Want to learn more about falling, and “the problem of the Moon”? Then definitely check out this superb Radiolab segment in their episode Escape, and another cool one on falling cats and why we fall.