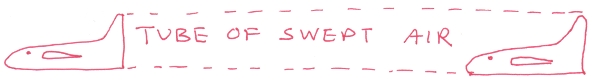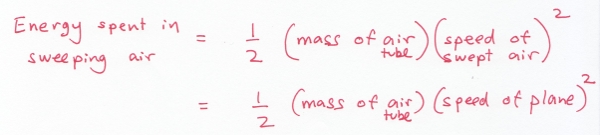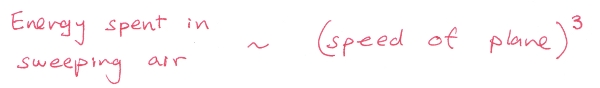Category: Biology

Can we build a more efficient airplane? Not really, says physics.

Update (13 October):  I emailed David MacKay to get his opinion on some of the critical comments responding to this blog post. David is a physicist at Cambridge University, author of the book ‘Sustainable Energy – Without the Hot Air’, and is the chief scientific adviser to the UK Department of Energy and Climate Change. You can read his response in the comments below. There’s also a interesting discussion of this post over at hacker news.

Boeing recently launched a new line of aircraft, the 787 Dreamliner, that they claim uses 20% less fuel than existing, similarly sized planes.

How did they pull off this sizeable bump in fuel efficiency? And can you always build a more fuel-efficient aircraft? Imagine a hypothetical news story, where a rival company came up with a new type of airplane that used half the fuel of its current day counterparts. Should you believe their claim?

More generally, do the laws of physics impose any limits on the efficiency of flight? The answer, it turns out, is yes.

Jet Man, by Ben Heine

There’s something about flying that doesn’t sit well with us. If we never saw a bird fly, it may never have occurred to us to build flying machines of our own.

Here’s where I think this sense of unease comes from. It takes stuff to support stuff. Everyday objects fall unless other things get in their way. Take the floor away, and you’ll plummet to your doom – the air below your feet isn’t going to do much for you. We move through air so effortlessly, that we barely notice it’s there. So what keeps a plane up? There doesn’t seem to be enough ‘stuff’ there to hold up a bird, let alone a Boeing aircraft weighing up to 500,000 pounds. To put that last number in context, its more than the weight of an adult blue whale!

Why is it that planes fly and whales typically don’t? The answer is easy to state, but its consequences are rather surprising. Planes fly by throwing air down. That’s basically it. It’s an important point, so I’ll say it again. Planes fly by throwing air down.

As a plane hurtles through the air, it carves out a tube of air, much of which is deflected downwards by the wings. Throw down enough air fast enough, and you can stay afloat, just as the downwards thrust of a rocket pushes it up. The key is that you have to throw down a lot of air (like a glider or an albatross), or throw it down really fast (like a helicopter or a hummingbird).

A physicist’s two-step guide to flight (it’s simple, really!)

Let’s make this idea more quantitative. Following David MacKay’s wonderful book on Sustainable Energy, I’m going to build a toy model of flight. A good model should give you a lot of bang for the buck. The means being able to predict relevant quantities about the real world while making a minimum of assumptions.

Toy models gone wrong. By Randall Munroe at XKCD.

Step 1: Sweep out a tube of air

As a plane moves, it carves out a tube of air. This air was stationary, minding its own business, until the airplane rammed into it. This costs energy, for the same reason your car’s fuel efficiency drops when you speed up on the highway. Your car has to shove air out of its way.

Exactly how much energy does this cost? You might remember from high school physics that it takes an amount of energy equal to 1/2 m v^2 to bring stuff with mass m up to a speed v.

In our case, we have

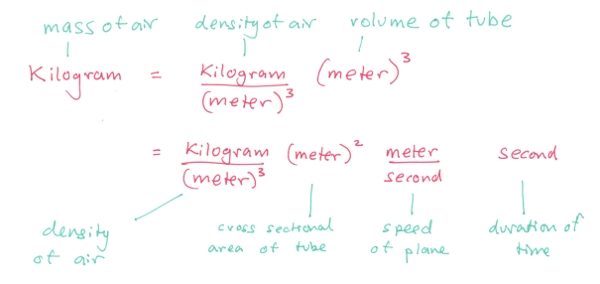
There’s still this mysterious factor of the mass of the air tube. To work this out, we can use a favorite trick in the toolbox of a physicist – unit cancellation. We can re-write the humble kilogram as a seemingly complicated product of terms.

What we’ve done here is to express an unknown mass of air in terms of other quantities that we do know. Each of these terms makes sense. Air that’s more dense will weigh more. A fatter plane (larger cross-sectional area) sweeps out more air, as does a faster plane. We’ve arrived at a meaningful result, just by playing around with units. In the words of Randall Munroe, unit cancellation is weird.

Put these two ideas together and here’s what you find:

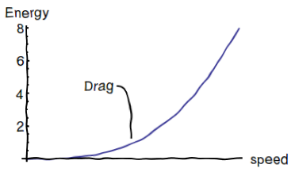
Here’s a graph of what that looks like.

If you’re with me so far, we just found that for a plane to plow through air, it has to expend an amount of energy proportional to the speed of the plane to third power. (The extra factor of v comes from the fact that faster planes sweep out a larger mass of air.) If you want to go twice as fast, you need to work 8 times as hard to shove air out of your way.

We’ve arrived at a general rule about the physics of drag. This holds true for a car on the highway, or for a swimmer or cyclist in a race. It’s why drag racing cars get only about 0.05 miles to a gallon! If we want to reduce overall energy consumption by cars, one option is to lower the speed limits on highways.

What does this mean for our toy plane? It would seem that the slower the plane, the higher its efficiency. So are airplane speed limits also in order? Absolutely not! To see why, read on to the second half the story..

Step 2: Throw the air down

In order to fly, a plane must throw air downwards. This generates the lift that a plane needs to stay up. It turns out that slower planes have to throw air harder to stay afloat. That’s why slow moving hummingbirds and pigeons have to flap their wings frenetically. It’s also why planes extend flaps while landing – they’re not throwing the air fast enough, so they compensate by throwing more of it.

More precisely, for a plane to stay afloat, the speed of the air jettisoned downwards must be inversely proportional to the speed of the plane. (You can take my word for this, although if you want to see where it comes from, take a look at David MacKay’s book.)

So we can now work out the second part of the puzzle. How much energy does it take to throw air down? As before, this is given by

Just as we did in the first step, let’s express things in terms of the speed of the plane.

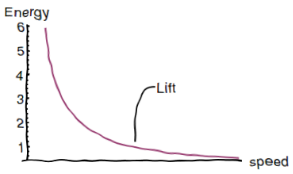
In words, the energy spent in generating lift is inversely proportional to the speed of the plane. Here’s what this looks like on a graph.

You can see from the plot that, as far as lift is concerned, slower flight is less efficient than faster flight, because you have to work harder in throwing air downwards.

There’s a lot to chew on here. To summarize, we’ve discovered that in making a machine fly, you have to spend energy (really fuel) in two ways.

  1. Drag: You need to spend fuel to push air away. This keeps you from slowing down.
  2. Lift: You need to spend fuel to throw air down. This is what keeps the plane afloat.

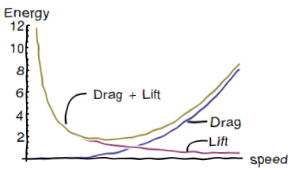
The total fuel consumption is the sum of these two parts.

If you fly too fast, you’ll spend too much fuel on drag (think of a drag racer or an F-16). Fly too slow, and you’ll have to spend too much fuel on generating lift, like a hummingbird furiously flapping its wings, powered by high calorie nectar. However, at the bottom of this curve there is a happy minimum, an ideal speed that resolves this tradeoff. This is the speed at which a plane is most efficient with its fuel. Be it through the ingenuity of aircraft engineers, or the ruthless efficiency of natural selection,  airplanes and birds are often fine-tuned to be as energy efficient as possible.

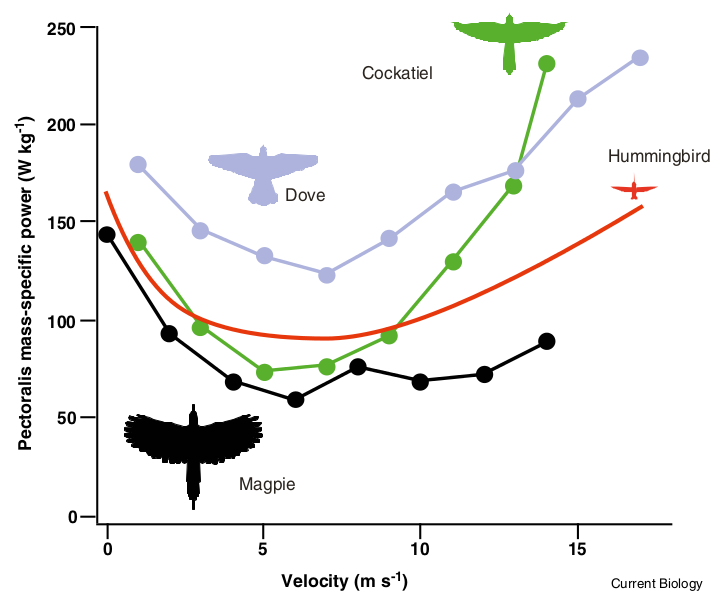
Here’s a plot of experimental data of the power consumption of different birds, as their flight speed varies.

You can see that it matches the qualitative predictions of the toy model.

But we can do more than this, and actually extract quantitative predictions from the model. An undergraduate schooled in calculus should be able to work out that special optimal speed at which energy consumption is a minimum. David MacKay plugs in the numbers in  his book, and finds that the optimal speed of an albatross is about 32 mph, and for a Boeing 747 is about 540 mph. Both these numbers are remarkably close to the real values. Albatrosses fly at about 30-55 mph, and the cruise speed of a Boeing 747 is about 567 mph. 

That’s a lot of mileage from a toy model!

And so our model teaches us that flying machines should never have speed limits. Whether made of metal or meat, every plane has an ideal speed. If you stray from this value, you have to pay for it in fuel cost. Slowing a car down may improve your mileage, but for a plane, the mileage actually gets worse.

And with this physicsy interlude into the world of albatrosses, hummingbirds, and jet planes, we come back to the question of the fuel efficiency of Boeing’s new aircraft.

You can actually use the model to work out the fuel efficiency of a plane. What you find is that it really just depends on a few factors: the shape and surface of the plane, and the efficiency of its engine. And of these factors, the engine efficiency plays the biggest role. So we would predict that engine efficiency, followed by improvements in body design might drive Boeing’s fuel savings.

This agrees with Boeing’s own assessment.

New engines from General Electric and Rolls-Royce are used on the 787. Advances in engine technology are the biggest contributor to overall fuel efficiency improvements.

New technologies and processes have been developed to help Boeing and its supplier partners achieve the efficiency gains. For example, manufacturing a one-piece fuselage section has eliminated 1,500 aluminum sheets and 40,000 – 50,000 fasteners.

Try as we like, we can’t squeeze a lot of improvement out of airplanes. Engines are already remarkably efficient, and you certainly can’t shrink the size of a plane by much, as economy class passengers can well attest. New manufacturing techniques could cut the amount of drag on the plane’s surface, but these improvements would only raise fuel efficiency by about 10%.

To quote David Mackay,

The only way to make a plane consume fuel more efficiently is to put it on the ground and stop it. Planes have been fantastically optimized, and there is no prospect of significant improvements in plane efficiency.

A 10% improvement? Yes, possible. A doubling of efficiency? I’d eat my complimentary socks.

References

I based this blog post on material I learnt from David MacKay’s fantastically clear book, Sustainable Energy without the Hot Air. It’s available online for free, and is highly recommended for anybody looking to use numbers to understand energy.

David MacKay (2009). Sustainable Energy – Without the Hot Air UIT Cambridge Ltd

I used this tip to make those XKCD style plots.

Milk, meat and blood: how diet drives natural selection in the Maasai

This post is a little different from the usual fare at this blog, as I am discussing a paper on which I’m a co-author. My collaborators and I just put up a paper in the open-access journal PLOS ONE. We analyzed genetic data from members of the Maasai tribe in Kenya and detected genes related to lactase persistence and cholesterol regulation that are under positive selection.

The Maasai and their Diet

Maasai tribe member drinking blood. Image credit: Rita Willaert

The Maasai are a pastoralist tribe living in Kenya and Northern Tanzania. Their traditional diet consists almost entirely of milk, meat, and blood. Two thirds of their calories come from fat, and they consume 600 – 2000 mg of cholesterol  a day. To put that number in perspective, the American Heart Association recommends consuming under 300 mg of cholesterol a day. In spite of a high fat, high cholesterol diet, the Maasai have low rates of diseases typically associated with such diets. They tend to have low blood pressure, their overall cholesterol levels are low, they have low incidences of cholesterol gallstones, as well as low rates of coronary artery diseases such as atherosclerosis.

Even more remarkable are the results of a 1971 study by Taylor and Ho. Two groups of Maasai were fed a controlled diet for 8 weeks. One group – the control group – was given food rich in calories. The other group had the same diet, but with an additional 2 grams of cholesterol per day. Both diets contained small amounts of a radioactive tracer (carbon 14). (You’d never get approval for a study like this today, and for good reason.) By monitoring blood and fecal samples, the scientists discovered that the two groups had basically identical levels of total cholesterol in their blood. In spite of consuming a large dose of cholesterol, these individuals had the same cholesterol levels as the control group.

Here is how the authors concluded their study:

This led us to believe, but without direct proof, that the Masai have some basically different genetic traits that result in their having superior biologic mechanisms for protection from hypercholesteremia

Motivated by these results, we set out to identify genes under selection in the Maasai as a result of these unusual dietary pressures. We scanned the genome looking for genetic signatures of natural selection at work.

The Data

Our data comes from the International HapMap Project, a collaborative experimental effort to study the genetic diversity in humans. The HapMap Project has collected DNA from groups of people from genetically diverse human populations with ancestry in Africa, Asia and Europe. Their anonymized data is publicly available for free. One of the HapMap populations is a group of Maasai from Kinyawa, Kenya  (n=156), and this is the population that we focus on.

DNA sequences on a part of Chromosome 7 from two random individuals, with the differences shown in red.

HapMap does not sequence full genomes, as this would have been prohibitively expensive at the time of data collection. Instead, they employ a shortcut. If you take my DNA sequence and line it up against yours, the two sequences will be about 99.9% similar. But every once in a thousand letters, or so, there will be a difference. You may have an A where I have a C. The HapMap group measures the DNA sequence at these very locations, where humans are known to vary from each other. In essence, they’re sampling the genome, looking only at sites where we expect to see variation. In the jargon of the field, this method is called looking for Single Nucleotide Polymorphisms, or SNPs (pronounced snips).

Hunting for signatures of selection in genetic data

Once you have the data, what can you do with it? We wanted to detect signs of natural selection. The basic idea behind detecting selection in genomic data is quite simple, and it has to do with sex. Every sperm or egg cell that you produce contains a single genome, which is formed by shuffling together the two sets of genomes that you inherited from your parents. Viewed this way, the role of sex is to shuffle together the genomes in a population into new combinations. If you compare the DNA sequences of a group of people, you will see signs of this shuffling.

The effect of sex is to shuffle genomes, in a process known as genetic recombination.

Now lets add natural selection to the mix. What happens if an individual is born with a new mutation that benefits their survival? Over time, you’d expect to see this mutation rise in frequency. Descendants of this individual will be over-represented in the population, as the fraction of people with this beneficial mutation goes up. In essence, the fingerprint of such selection is a reduction of genomic diversity. (I’m describing a particular model of selection here, known as positive natural selection. Some other types of selection can increase diversity, such as the selection on viruses to evade recognition by their host’s immune system.)

A new beneficial mutation arises in an individual (shown in red). It will rise in frequency in the population, leading to a characteristic reduction in diversity. Over time, genetic recombination and new mutations will build back the diversity, and the signal is lost.

Eventually, new mutations will creep in again, and generations of sexual reproduction would build back the diversity. However, if the loss of diversity was sudden enough (strong selection) and not too long ago, you can still detect it today. There are statistical tests (Fst, iHS, XP-EHH) that can formally detect if the reduction in diversity at a given region is sufficient to infer selection. Sabeti et al have a nice review paper that discusses the different methods available to detect selection using genomic data.

Our Results

We used three different methods to detect selection, and our top candidate regions under selection are considered significant by at least two of the methods.

The strongest signal of selection, detected by all 3 methods, was a region on Chromosome 2 containing the Lactase gene (LCT), responsible for breaking down the lactose present in milk. Mutations in a neighboring gene in the cluster, MCM6, are associated with the ability to digest lactose in adulthood.

The strongest signal of selection was a region on Chromosome 2 that contained the LCT gene producing lactase, the enzyme that breaks down the lactose in milk. Interestingly, the default state in all adult mammals is to stop producing lactase in adulthood – our ancestors were all ‘lactose intolerant’. This makes sense from an evolutionary point of view, it forces children to wean from milk, and frees up the mothers resources. It turns out that different sets of mutations arose that gave European and African pastoralists the ability to digest milk. Those of us whose ancestors weren’t pastoralists still have trouble digesting milk.

This is a classic example of a selective sweep – a mutation confers an advantage (the ability to digest milk), and then sweeps through a population like wildfire. This result has been previously described in European populations, and also in African populations (including the Maasai) by Sarah Tishkoff and collaborators. Given that the Maasai consume large amounts of milk, it is not surprising that we see a very strong signal at this locus. We sequenced DNA in this region to confirm this result and, sure enough, we found that one of the lactase persistence conferring mutations identified by Tishkoff was present in the HapMap Maasai samples.

Two of the tests for selection that we used require that you make comparisons with another population. We chose the Luhya of Kenya as a our reference population. Among all the protein-altering mutations present in the data, the one that showed the largest population difference between the Maasai and Luhya (as measured by Fst) sits in the gene for a fatty acid binding protein FABP1. This protein is expressed in the liver, and the variant that occurs at higher frequency in the Maasai is associated with a lowering of cholesterol levels in Northern German women (n = 826) and in French Canadian men consuming a high fat diet (n = 623). Furthermore, studies in mice fed a high fat, high cholesterol diet showed that deactivating the FABP1 protein leads to protection against obesity, and lower levels of triglycerides in the liver, when compared to normal mice on an identical diet. These results suggest that this protein plays a role in regulating lipid homeostasis, and its selection in the Maasai may be diet-related.

On Chromosome 7, two of the methods we used to detect selection identified a cluster of genes that fall in the Cytochrome P450 Subfamily 3A (CYP3A). This family of genes is involved in drug metabolism, in oxidizing fatty acids, and in synthesizing steroids from cholesterol.

What’s next?

Computational methods can only take you so far. We have identified genes in candidate regions undergoing positive natural selection in the Maasai, possibly arising due to their unusual diet. But the case for selection can only be definitively made with an experimental study targeted to address the role of these genes in maintaining cholesterol homeostasis. We’re hoping to collaborate with experimental biologists to take these hypotheses forward and investigate their role in the evolutionary history of the Maasai.

So head over to PLOS, check out the paper, and let us know what you think.

Update: Here’s another blog post that discusses the paper, focusing more on the mixed genetic makeup of the Maasai.

References:

Kshitij Wagh, Aatish Bhatia, Gabriela Alexe, Anupama Reddy, Vijay Ravikumar, Michael Seiler, Michael Boemo, Ming Yao, Lee Cronk, Asad Naqvi, Shridar Ganesan, Arnold J. Levine, Gyan Bhanot (2012). Lactase Persistence and Lipid Pathway Selection in the Maasai PLOS ONE, 7 (9) : 10.1371/journal.pone.0044751

If you’d like to read more about selective sweeps, you may enjoy my post Why moths lost their spots, and cats don’t like milk. Tales of evolution in our time.

Towards nature’s fastest draw

It’s not easy to move fast. I say this not just out of laziness. The fact is, in the animal kingdom, moving quickly comes at a considerable energy expense. It also tends to wear down muscles and joints. So you can be pretty sure that whenever you see an animal that’s clocking in at a record speed, it’s doing so for a very, very good reason.

Take the case of the mantis shrimp. These incredible crustaceans come in two varieties: stabbers, and smashers. Sheila Patek is a biologist who studies them for a living. In a fascinating TED talk from 2004, she describes how mantis shrimp have the fastest blow in the animal kingdom. Their strike force is so great that it creates a visible shock wave in water, in a bizarre phenomenon known as cavitation. Patek goes on to describe the engineering solutions that these animals use to create and sustain their powerful smash.

I may not know karate, but I know crazy.

Since 2004, the list of nature’s fastest has had more than a few additions. It’s the time of the year for holiday lists, so I decided to list some of the most impressive record holders in this regard. To do this, I relied mainly on references I found on the wonderful website of Patek’s lab.

The life forms that follow are pushing the limits of physics and engineering. Typically, they are doing this to rein death and terror onto hapless prey. They are the Terminator 2’s of our world. So please join me, as we descend down this list towards the most lethal of all blows. This is a quest for the fastest draw in nature.

But first, let’s start with something fast that we’re familiar with. When talking about short intervals of time, we often use the phrase ‘in the blink of an eyelid’. The time it actually takes us to blink an eyelid is about 3 tenths of a second or 300 milliseconds.

A blink of an eye  (300 milliseconds)

So, our first point of reference is 10 milliseconds, or 1/30th of a blink of an eye

The ballistic tongue of the salamander (< 10 milliseconds)

The explosive tongue of the giant palm salamander of Central America bursts out in under 10 milliseconds, targeting flying bugs that don’t know what hit them. To achieve this feat, the tongue of this cold blooded sniper needs to output energy at the rate of a whopping 18,000 Watts per kilogram of muscle.

It stores this energy like a tightly coiled spring. As it relies on the principle of a slingshot, it can even operate in cold temperatures when muscles are slow to contract.

This tongue has been called the world’s most powerful muscle, but it’s no comparison to what follows.

The vacuum suction of the anglerfish (<5 milliseconds)

An anglerfish has what seems like a rather improbable fishing strategy.

You couldn't dream this stuff up. Source: NOAA photo library

It lures its prey in with a shiny dangling object attached to its head. All of a sudden, its mouth expands to more that 12 times its original size. The low pressure region thus created sucks in water at great speed, as well as whatever unfortunate fish happens to be swimming nearby. It’s a process that looks alarmingly like this.

And this strange kiss of death can take place in less than 5 milliseconds, or 1/60th of a blink of an eye.

The blinding strike of the mantis shrimp (2.7 milliseconds)

This has to be one of the most impressive punches in nature.

Sheila Patek and collaborators measured that the blow of the mantis shrimp can reach a peak speed of 51 mph (23 m/s), in less than 1/100 of the blink of an eye. All this while underwater! It’s so fast that it actually creates a visible shock wave. Meanwhile, its limb experiences over 10,000 g of acceleration.

When you can wield a shock wave, you qualify as badass. Source: Patek et al, Nature 428, 819-820 (2004)

To put this number in context, think of this: a typical person can handle an acceleration of about 5 g before losing consciousness, while decelerations of 100 g are about the highest that humans have survived, in Indy car racing accidents. A bullet shot out of a Beretta gun is accelerated by about 40,000 g.

If you were a snail or a clam, this could well be the last thing that you see:

Needless to say, a mollusk doesn’t stand much of a chance against this punch. The muscle that powers this impressive blow is delivering a mind-numbing 470,000 Watts per kilogram. It’s quite literally blowing the competition out of the water.

Well.. not quite. Read on.

Continue reading Towards nature’s fastest draw

What it feels like for a sperm, or how to get around when you are really, really small

This post was chosen as an Editor's Selection for ResearchBlogging.orgWe don’t usually learn about the physics of squishy things. Physics textbooks are filled with solid objects such as incompressible blocks, inclined planes and inelastic strings. This is the rigid world that obeys Newton’s laws of motion. Here, squishiness is an exception and drag is routinely ignored. The only elastic object around is a spring, and it is perfectly elastic. It will never bend too far and lose its shape. But any child who has played vigorously with a Slinky has stretched past the limits of this Newtonian world.

Mr. Newton's not going to like that..

Whereas the rigid universe is notable for its strict adherence to a few basic principles, the squishy universe is a different beast altogether.

I was recently out paddling, and noticed that as you move the paddle through water, tiny whirlpools begin to develop along its sides. The whirlpools grow in size, become self-sustaining, and break off and float away. Eventually they die out, as they lose their energy to the fluid around them.

You could also watch the spirals and vortices created by rising smoke. Or notice the strange shapes made by the wind as it sweeps through the clouds. It’s as if fluids have a life of their own, often wondrous and beautiful, and other times surprising and counter-intuitive.

The brief and wondrous life of vortices

But the motion of fluids is notoriously hard to predict. It’s so difficult that if you can solve the equations of fluid flow, there are people willing to offer you a million dollars. The difficulty comes from a mathematical property of the equations known as non-linearity. Simply put, a non-linear system is one where a small change can lead to a large effect. The same thing that makes these equations difficult to solve is also what makes fluids surprising and interesting. It’s why the weather is so hard to predict – tiny changes in local temperatures and pressures can have a large effect.

At this point, most reasonable people would throw their arms up in despair. But physicists are an unreasonably persistent bunch, and when faced with an equation that they can’t solve, they try to get some insight by looking at what happens at extremes. For example, thick and syrupy fluids like glycerine behave in a surprisingly orderly fashion. Take a look at this video (watch through to the end, it’s worth it).

I bet you’ve never seen a fluid do that before. So what’s going on here? And what does this have to do with swimming sperm?

Continue reading What it feels like for a sperm, or how to get around when you are really, really small

Honeybees have handy knees!

A few days ago, I was walking home and passed by a bush of white flowers in full bloom. They looked pretty spectacular lit by the afternoon sun. On taking a closer look, I realized that what I thought were flowers were actually flower bunches, each of them made up of hundreds of tiny flowers. And on each bunch, there was a single honeybee zipping about from flower to flower.

Watching these bees through my camera lens, I could see something quite interesting. As they landed on the flowers, they would kick up grains of pollen that would rise up like dust. And then the bees would do something quite odd – they would fiddle with their knees. I zoomed in to see what was going on.

There’s something quite peculiar about this photograph. What’s that fleshy appendage stuck to the knees of the honeybee? It looks, to me, somewhat like a human ear. And even stranger – the bees don’t have it when they arrive on the flower. But in a few minutes this thing begins to grow, and in about 15 minutes it’s as engorged as you see in the picture.

In addition to collecting nectar from flowers, honey bees also collect pollen. And what you’re seeing in these photographs is an incredible adaptation that helps bees go about their business of collection. It’s called a pollen basket, and here is how it works.

Bees are hairy creatures, and they get covered in pollen. They rake themselves clean with combs that are built into the inner surfaces of their hind legs. Next, they move all this collected pollen to a joint between the segments of their legs – their knees. This joint functions as a pollen press, and it squeezes the pollen into handy little pellets. But these pellets need to be stored somehow. And so, here is the next adaptation. The outer surface of the hind leg is concave, and it is covered in many small hairs. It’s a basket! This is where the bees store these compressed pollen pellets, and that’s what you see in the above picture. The basket is actually transparent, and so the fleshy color in the pictures above is the color of pollen.

The weird thing about this is that the basket is open at the bottom. So why doesn’t the pollen fall out? That’s because there’s a single strong hair that prevents this from happening, which functions as the lid of the basket.

Although I couldn’t quite make out the details, watching this elaborate packing process through the zoom lens was quite mesmerizing and I was merrily snapping away. The bees didn’t seem to notice me at all, but I realized that I was getting odd looks from my neighbors, so I decided it was time to take my leave.

Buzzing off..

Dissecting the language of the birds, or how to talk to a songbird

The Norse god Odin had two songbirds, named thought and mind, whose daily tweets were the source of his knowledge on our mortal affairs.

Young children have an uncanny ability to pick up new languages. Not only do they soak up vocabulary, they also construct new sentences of their own. This ability to use grammar is the essence of language. It’s not enough to know the meanings of words, you also have to understand the structures and rules by which words are put together.

The predominant view has been that humans are unique in this ability. But any time that we utter the words ‘uniquely human’, scientists seem to take it as a challenge to disprove this notion. And language is no exception. If you’re looking for the species that most closely matches our linguistic prowess, surprisingly, you won’t find it in the apes, the primates, or even in the mammals. You have to travel to a far more distant relative, all the way to a family of birds known as the songbirds.

The vocal life of a songbird is similar to ours in many ways. They learn songs by imitating their elders. Like human speech, these songs are passed down from one generation to the next. Songbirds are also best equipped to learn songs in their youth, and they have to practice to develop their ability. They can improvise and string together riffs into new songs, and over generations these modified songs can turn into new dialects. And like us, they come hard-wired with ‘speech-centers’ in their brain that are dedicated to language processing.

But languages are not just learned, they can also be invented. A striking example comes from the deaf community of Nicaragua in the 1970s. Back then, deaf people in Nicaragua were isolated both physically and through language. By the 1980s, the government set up schools for the deaf to teach them Spanish and how to lip-read. This turned out to be an unsuccessful endeavor. The teachers were growing increasingly frustrated as they were not getting through to the students.

However, things were quite different from the point of view of the students. For the first time, they were in contact with many other deaf people, and they started to exchange gestures that they had invented in isolation. At first the teachers thought this gesticulation was a kind of mime, but the reality was far more interesting. By getting together and pooling their ideas, these children had actually invented a new type of sign language, complete with its own grammatical structure. Here was proof that a new language could be born out of cultural isolation, a testament to our innate abilities to understand grammar. And in a few generations, users of this language were employing newer, more nuanced grammatical structures.

And this re-invention of language has been mirrored in the songbirds. An experiment from 2009 by Fehér and colleagues took newly hatched songbirds of the zebra finch species and raised them in sound proof chambers. They did this during their critical period of language development. Much like the Nicaraguan children, these birds were raised in a world without song. What happened next is quite surprising.

Continue reading Dissecting the language of the birds, or how to talk to a songbird

Marine animals save energy by coasting like birds

It feels good to be an animal. Unlike trees that are tethered to the ground, we animals have the incredible ability to travel. And we do so in a variety of ways. Some like to walk, others run. Others get around by swimming or flying. There are climbers, leapers, and hoppers, and others that prefer to roll and tumble.

Locomotion certainly affords us a great deal of freedom, but it comes at a considerable energy cost. Through countless generations of incremental evolution, our bodies have arrived at many solutions to balancing our energy budget. Fish have streamlined profiles, birds have hollow bones to stay light, and kangaroos have spring loaded hind legs that seamlessly capture and release the energy needed for flight. In the African savannah, predators chase down their prey using long, muscular legs that give them an efficient stride.

In addition to changes in form, animals can also use strategies to travel more efficiently. Birds that need to fly a long distance often make use of a curious technique. They flap their wings to gain height, and once they builds up enough height, the wings stop moving and they glide back downwards. Many birds repeat this wave-like motion in flight, instead of flying at a fixed altitude.

It’s like the difference between cycling on flat terrain or on an undulating, hilly road. In one case you pedal at a steady pace, in the other you alternately pedal hard and don’t pedal at all. The reason that birds adopt this undulating flight strategy is that it saves them energy.

But what’s special about air? What about animals that live in water? In the ocean, swimming is the equivalent of flying. So do marine animals adopt similar swimming strategies to conserve energy? To answer this question, an international group of researchers led by Adrian Gleiss attached sensors onto sharks and seals. They monitored the swimming motion of the whale shark, the white shark, the northern fur seal, and the southern elephant seal.

Here is an animation that they made directly from their recordings, that shows a whale shark swimming.

Continue reading Marine animals save energy by coasting like birds

Why have sex? To fight parasites, of course!

This post was chosen as an Editor's Selection for ResearchBlogging.orgThis post was selected by Vincent Racaniello as an editor’s selection on ResearchBlogging.org The (revised) title of this post was suggested by Lucas Brouwers. Check out his excellent blog on evolution, Thoughtomics.

New Zealand mud snails, before and after infection by parasites. These tiny creatures may move slowly, but peering beneath the surface reveals an incredible race for survival.

Why do we have sex? If this question keeps you up at night, you either have really loud neighbors, or you have the makings of an evolutionary biologist. Some of the most brilliant minds in the field – William Hamilton, John Maynard Smith and George Williams – have spent much of their careers wondering about the value of sex. This is not a reflection on the quality of their sex lives. Rather, it has more to do with their creative insight and ability to look at the world with fresh eyes.

A billion years ago, our ancestors inhabited a world without sex. This was the era of the clones. In this strange world, all organisms reproduced by creating identical genetic copies of themselves, somewhat similar to how modern-day bacteria reproduce [1]. But this clonal strategy has a problem. Populations made up of identical twins are more vulnerable to infection. When a disease comes along, it doesn’t just wipe out a few individuals. It can take out the whole lot.

When sex arrived, it introduced a new pace to life. Organisms were mixing and matching genes in combinations never seen before. Imagine a world where you had to dress well to survive. In such a world, the invention of sex is like going from wearing uniforms to having your own wardrobe. You could pick a gene from here, another from there, and put together a novel offspring. And if a particular outfit were deemed ‘unfit’, it’s not a huge tragedy as there are plenty of alternatives.

In this way, sex helps us by innovating new evolutionary solutions and by protecting us from disease. But sex is not without its discontents. For one thing, sexual reproduction implies that you only pass down half your genes to your offspring. The other half come from the other parent, and they combine to make an offspring with a full set of genes. On the other hand, in asexual reproduction, the mother passes on a full set of genes to her offspring. So by adopting sex, your genes are travelling half as far. In evolutionary terms, this is a huge cost, and sex had better have a lot to offer for it.

John Maynard Smith described "the two-fold cost of sex" - Asexual populations (b) grow twice as fast as sexual populations (a).

Do the benefits outweigh the costs? We would certainly like to think so. But when evolutionary biologists did the math, they worked out that the answer is usually no. Your genes typically have more to gain if you reproduced asexually.

So what gives? Why, then, do so many species adopt a sexual lifestyle? Well, here’s a brilliant solution offered by Hamilton and others: if you are under constant attack by rapidly evolving parasites, then sex is a better strategy than cloning yourself. This idea came to be known as the Red Queen hypothesis and can be summarized in one line: it’s harder to hit a moving target.

"Now, here, you see, it takes all the running you can do, to keep in the same place."

Continue reading Why have sex? To fight parasites, of course!

Why moths lost their spots, and cats don’t like milk. Tales of evolution in our time.

In the children’s game of hide-and-seek, it doesn’t matter much whether you win or lose. In the animal kingdom, however, the stakes are significantly higher. If you’re found, you’re food.

And death is not just the end of the individual, it’s the end of a lineage. Organisms that die before they can reproduce deny their genes a road to the next generation. In this simple fact lies the engine of change. For example, genes that make a prey more camouflaged will end up increasing their reproductive success, whereas genes that make them more noticeable are not going to get very far. In this way, natural selection is driving prey to become better hiders, and predators to become better seekers.

Nowhere is this evolutionary race more evident than in the case of the peppered moth. This is a species of moth that is found all across England and Ireland. When people first studied them in the early 1800s, almost all the moths looked something like this:

As you can see (if you’re looking closely), the white and black speckles are effective camouflage. For ages, these moths have hidden on light colored trees and lichens. Over time, they have evolved this distinctive pattern to help them evade the notice of the birds that prey on them.

But just fifty years later, things were beginning to change. By the 1850s, moths of the same species had stumbled upon a new color. These new moths were called carbonaria after their carbon-black color, to distinguish them from their salt-and-pepper colored relatives with the dull name typica.

By the end of the nineteenth century, the change was drastic. In 1895, a study in Manchester showed that 95% of the peppered moths were now of the black type. So what was going here? What could cause such an incredible change in appearance in just a hundred years?

Continue reading Why moths lost their spots, and cats don’t like milk. Tales of evolution in our time.

Destroying the disposers of death: will India rescue its few remaining vultures?

Indians today can hardly recall the last time that they saw a vulture. In the 1990s, these majestic birds were a common sight in the subcontinent, and would show up wherever there was exposed carrion. As a child, I remember marveling at vultures circling at impressive heights, probably looking back down at me with their incredible eyesight, their wings outstretched as they effortlessly hovered on columns of warm air.

But since the nineties, their numbers have been falling dramatically in India, Pakistan and Nepal. The scale is astonishing – for every thousand white-rumped vultures in 1990, only one is alive today. A similarly sad story holds for the Indian vulture and the slender-billed vulture. Together, all three Asian vultures are now listed as being critically endangered.

The White rumped vulture, Gyps bengalensis

So what’s going on? It’s not that they are being hunted. For one thing, the killing of all wild animals in banned in India. But also, vultures have always provided a much valued ecological service. Most villagers dispose of dead animals by dumping the carrion. And they rely on the vultures to clean up.

Vultures have an undeservedly bad reputation. Because we associate carrion with disease, people believed that vultures spread diseases. But in fact, we now know that the opposite is true. Their powerfully corrosive stomach acids allow them to safely digest carrion that would be lethal to other scavengers, wiping out bacteria that can cause diseases like botulism and anthrax. They are the purgers of death and disease.

In their absence, populations of feral dogs have exploded, bringing with them the threat of rabies and human attacks. And if rats follow suit, India would face a new public health nightmare as it tries to control the spread of rodent-borne diseases like bubonic plague [1].

Continue reading Destroying the disposers of death: will India rescue its few remaining vultures?